Functional programming (FP) is all about writing software using immutable values and pure functions. These two fundamentals give way to more complexity the deeper you go into the subject. I found that using mathematics, specifically algebra, made it easier for me to grok what I was seeing while working with Scala and Elm.
Immutability
Let’s start with the concept of immutability. If something is immutable, it means that it cannot change. On its own, it doesn’t seem like much, but when applied to a programming paradigm it becomes extremely powerful. Let’s take a look at an example:
var a = "Hello there";
var b = " and goodbye";
a += b;
Console.println(a); // "Hello there and goodbye"
Here, a is mutable. Its value is being changed — and, notably, Scala’s var
declaration allows you to change it. With languages like
Elm, which is a functional language, you cannot do
something like this.
When I first came across immutability, I found it difficult to justify why it was so important. This is where algebra comes in.
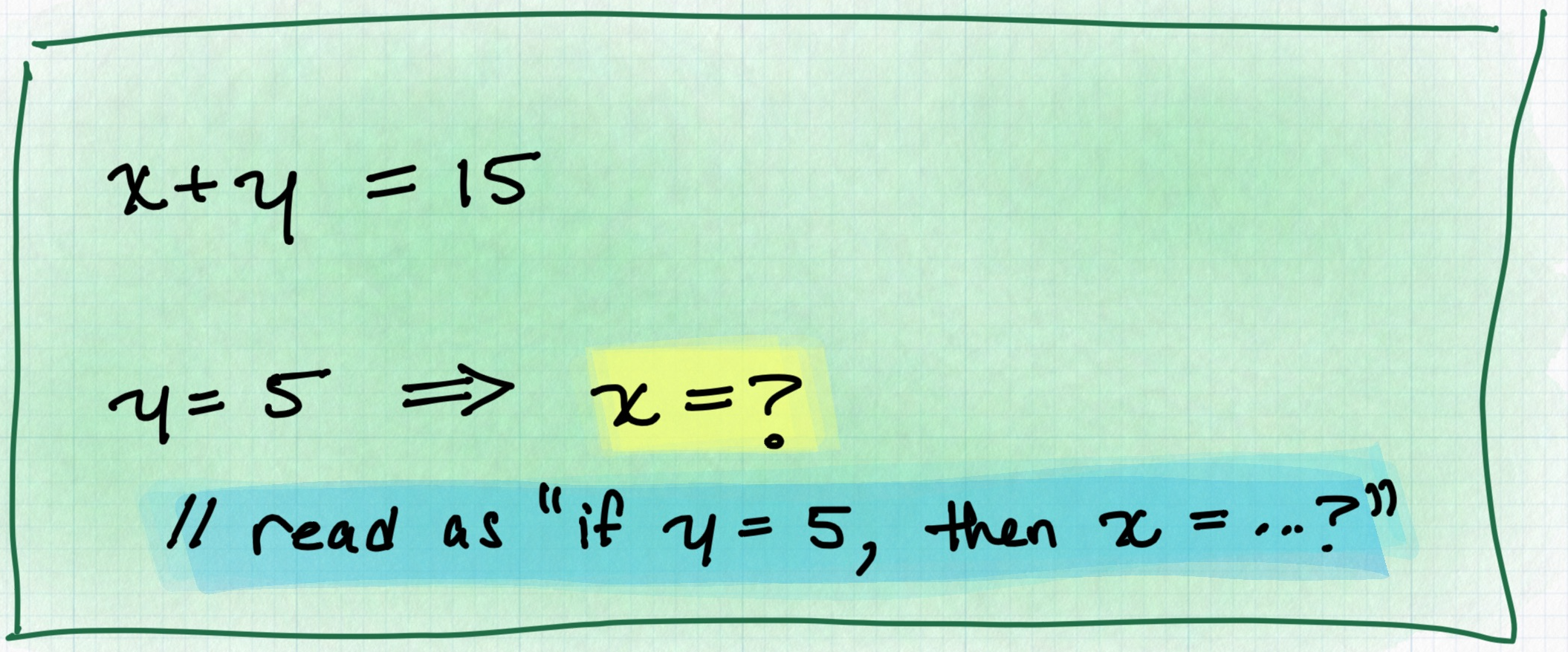
How did you step through solving this problem? Did you take the value of y for
granted and expect it never to change?
Now, what if you didn’t take y = 5 for granted? Could you get a numerical
answer for x?
No.
(At least not in a way that wouldn’t require you to reconsider how you defined “numerical”. But that should be left to the math textbooks.)
In your run-of-the-mill, non-functional program, not using immutible values is
the equivalent of always changing the value of y in this algebra problem. This
increases mistakes and clouds readability. A better way to write the Scala
example would be as follows:
val a = "Hello there";
val b = " and goodbye";
val allTogether = a + b;
Console.println(a); // "Hello there"
Console.println(allTogether); // "Hello there and goodbye"
The bonus here is that you still have the original copy of a, which you could
now use if you wanted to make a more complex program. For example, you could
make a greeter.
If someone is approaching the greeter, the greeter could say “Hello there” and if they are leaving the greeter, they could say “goodbye”. Then, if someone is running past the greeter, you might want the greeter to say both!
In the first run of the older version of this program, a would’ve been
reassigned to “Hello there and goodbye”, which would’ve broken the greeter!
In Scala, the way you designate immutable values is through the use of val.
val a = "Hello there!"
a = "Goodbye!" // error: reassignment to val
I am blocked from reassigning a variable if I’m using val. Pretty sweet,
right? If I don’t want to be blocked, I could always use var, but that’s how
you get 🐛🐜🐞 – and end up with an impossible algebra problem!
Pure Functions
If immutability is the potatoes of this operation, then pure functions are the meat (or the tofu for the plant-eaters). As before, I think it’s useful to return to algebra to understand what pure functions actually are. An example like this really helped me visualize them:

f(x), pronounced “function of x” and more often “f of x”, here is x + 5. So,
f(6) = 11. I will never expect x = 6 to give me any other answer than 11
for this function. Why? Because this function is pure:
For a function f(x) = y, x will always return y no matter how many times
you call the function.
Here, y is just x + 5, but it could be anything. It could be cos(x) or
abs(x); it doesn’t matter.
Similar to immutability, on their own, pure functions don’t look powerful: they just look like algebra.
All told, though, good FP is just algebra.
By defining a pure function as something that will yield a predictable value every time, because the same input should always return the same output, you suddenly are left with one less unknown.
Debugging becomes easier and testing edge cases are no longer a Heruclean task. You can also feel better about composing larger, more complex functions out of smaller ones. Of course, algebra also can do function composition.
Here is an example:

Here, f(x) is x + 3 and g(x) is 2x + 1. Composing them is simply putting
one of the functions inside the other. So, you can have f(g(x)) (pronounced “f
of g of x”) or g(f(x)) (“g of f of x”).
If we solve f(g(x)) for when x = 3, then we first do g(3), which is 7.
Then we do f(7), which is 10.
Since both f(x) and g(x) are pure functions, you can also conclude that
their composition will also be pure. That gives you greater security when
solving this problem.
The same goes for function composition in FP as well! If you are working with two pure functions then, when you compose them, then you can guarantee the same output given the same inputs.
Here is an example:
val doubleInt: Int = (x: Int) => x * 2
val addOne: Int = (y: Int) => y + 1
doubleInt(addOne(3)) // doubleInt(3 + 1) => doubleInt(4) => 8
addOne(doubleInt(3)) // addOne(3 * 2) => addOne(6) => 7
Here, doubleInt(addOne(3)) will always give you 8 and
addOne(doubleInt(3)) will always give you 7. That is, unless you update
one of the functions directly!
That’s pretty comforting especially when you find yourself moving beyond the simple arithmetic in these examples.
Closing Notes
As stated previously, good FP is algebra. Because of that, when learning why the fundamentals of FP are so important, it’s useful to look at the mathematics behind it.
Hopefully this rekindled some of the joy you might’ve felt in your math classes of years past. If not, then know you can enjoy programming without having to look back at those tumultuous times. 😆
