I recently discovered a new way to trigger a stack overflow in Elm - chaining 10K random generators 🙈
Understanding why this happens and how to resolve it was quite the journey. Along the way I had to bust out several different debugging techniques including proving myself wrong and reasoning by analogy.
-- Fine with 1K, stack overflow for 10K
sprawlOut : Int -> Location -> Generator ( Location, Set Location )
sprawlOut depth loc =
List.foldl
(\_ acc -> R.andThen sprawl acc)
(R.constant ( loc, Set.empty ))
(List.range 1 depth)
sprawl : ( Location, Set Location ) -> Generator ( Location, Set Location )
sprawl ( loc, set ) =
R.uniform loc (neighborsOf loc)
|> R.map (\next -> ( next, Set.insert next set ))
See the full original problem in action
Simplify the problem
That random generator is intimidating! 😱😱😱
It’s doing two things: generating locations (via the sprawl generator), and
accumulating them in a set.
It might be easier to figure out the answer if we work with a simpler problem.
Let’s replace that sprawl generator with one that generates random numbers.
dieRoll : Generator Int
dieRoll =
Random.int 1 6
We can extract the accumulation part to a separate function and use a plain old
list instead of a Set. Also, it turns out all the rolls are independent so we
can use map2 instead of andThen.
combine : List (Generator a) -> Generator (List a)
combine =
List.foldl (Random.map2 (::)) (Random.constant [])
Put those two together, our simplified problem looks like:
-- Stack overflow!
List.map (always dieRoll) (List.range 0 10000)
|> combine
We’re still getting a stack overflow. That’s good! If we didn’t that would mean we’d oversimplified, and removed something essential to reproducing the bug along the way. As it stands, if we can find a way to generate 10K random die rolls, we’ll also be able to use the same solution to fix our original problem.
See the simplified problem in action.
Construct experiments
Make a guess about why things are breaking. Then try to prove yourself wrong!
Building up large lists of generators cause stack overflow
-- Works fine
List.map (always dieRoll) (List.range 0 10000)
This doesn’t stack overflow so that’s not the cause of our error.
Process of elimination
Time to scale! List some of the possible reasons the code might be broken, then try to prove them all wrong. At each step you’ll learn something new.
We’ve already proven that building a large list of generators is fine. The error
must be in combine.
Looking into the implementation, three possibilities jump to mind:
::breaks on large listsList.foldlbreaks on large listsRandom.map2 (::)breaks on large lists
Lets try to prove all them wrong!
-- No problem!
0 :: (List.range 1 10000)
-- No problem!
List.foldl (::) [] (List.range 1 10000)
-- No problem!
Random.map2 (::)
(Random.constant 0)
(Random.constant <| List.range 1 10000)
Hmmm, all of the individual pieces work fine on their own. Maybe the problem lies with how they play together 🤔
How are things the same?
combine is a pretty common function that can be defined for many types. For
example, you could also define it for Maybe:
combineMaybes : List (Maybe a) -> Maybe (List a)
combineMaybes =
List.foldl (Maybe.map2 (::)) (Just [])
and for Result
combineResults : List (Result e a) -> Result e (List a)
combineResults =
List.foldl (Result.map2 (::)) (Ok [])
Time for a new hypothesis:
There is a fundamental flaw in the algorithm for
combinethat breaks down at larger list sizes.
Let’s try to disprove it!
-- No problem!
List.map Just (List.range 1 10000)
|> combineMaybes
-- No problem!
List.map Ok (List.range 1 10000)
|> combineResults
Hmmm, combine seems to be working fine here. Let’s try with a more complicated type for good measure:
-- Stack overflow!
List.map Decode.succeed (List.range 1 10000)
|> combineDecoders
Huh, why does combine fail for large lists of generators and decoders but not
for maybes and results? Or put differently, how are the Generator and
Decoder types similar to each other, but different from Maybe and
Result?
Looking at the source for Random, we can see that Generator is actually a
function under the hood:
type Generator a =
Generator (Seed -> (a, Seed))
and Random.map2 chains those functions under the hood to thread the Seed
to both generators.
The Decoder type is implemented in JavaScript for efficiency, but if one were
to implement it in Elm it would also be a function under the hood:
-- What a pure Elm implementation could look like:
type Decoder a =
Decoder (Value -> Result Error a)
So it looks like combine breaks on types that wrap a function. That’s
surprising. It would be like saying that composing a function 10K times doesn’t
work!
Just for thoroughness, let’s try to prove that last statement wrong:
increment n = n + 1
-- Stack overflow!
List.map (always increment) (List.range 1 10000)
|> List.foldl (<<) identity
🤯🤯🤯
This is HUGE! Not just because I made an incorrect assumption (it happens!), but because this discovery is going to enable me to bring a powerful debugging technique to bear - reasoning by analogy.
Reasoning by analogy
Reasoning by analogy is a problem-solving technique that goes like this:
- You have a hard problem you don’t know how to solve
- Find an easy problem that’s similar
- Figure out the answer to the easy problem
- Use the same solution to solve the hard problem
We’ve already reached for a variation of this technique when we simplified our generator right at the beginning! Our hard problem is “generating the complex set of locations causes stack overflow for large sizes”. We simplified it to “generating 10K random numbers causes stack overflow”. If we can solve that, then we can retrofit the solution onto our original hard problem.
However, even our “easier problem” is proving difficult to solve. We’ve used some other debugging techniques to eliminate some possibilities and gain better understanding of what might be causing the problem.
We’ve also discovered an even easier problem that’s similar: “composing a large
number of functions causes a stack overflow”. This time however, it’s a problem
we already know the solution to! It’s definitely possible to increment 10K
times in a stack safe way.
We can do this as a recursion or via
List.foldl:
-- Works fine!
List.range 1 10000
|> List.foldl (\_ acc -> increment acc) 0
So what’s the difference between this and folding <<? Let’s look at each step
of the loop:
-- List.foldl (<<)
--
-- Each step composes `increment` and the
-- return of the previous step
(x -> increment x)
(x -> increment (increment x))
(x -> increment (increment (increment x))
(x -> increment (increment (increment (increment x))
...
-- stack overflow!
-- List.foldl (\_ x -> increment x)
--
-- Each step increments the return of the previous step
0
1
2
3
...
10000
When folding composition, we’re building a giant nested function but we never execute any of the steps. 10K nested function calls is enough to blow the stack on my machine.
When folding increment directly, we’re eagerly evaluating each step. We
aren’t building deeper and deeper functions, instead we do the work immediately
at each step and increment the number.
Now that we have some facts, let’s do some reasoning! Given that:
- 10K chains of
Random.map2causes a stack overflow - 10K compositions of
incrementcauses a stack overflow - I can call
increment10K times on itself if each step is eagerly evaluated.
Therefore (by analogy) I should also be able to accumulate the results of 10K random generators as long as each step is eagerly evaluated.
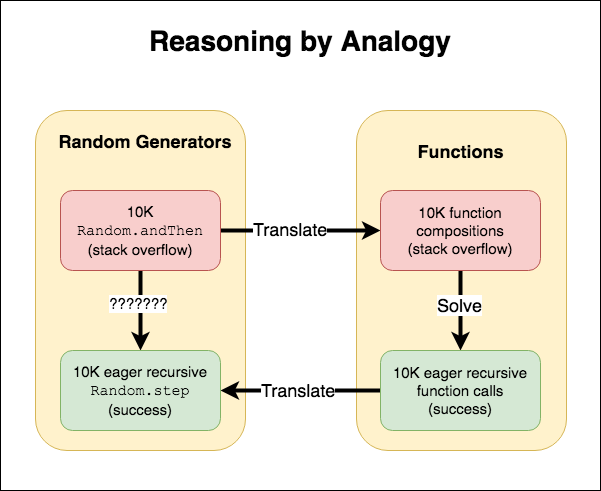
Working our way back to the original problem
So how does one “eagerly” evaluate a random generator? If we have a seed we can
use Random.step to manually evaluate the generator, giving us back a random
value immediately.
Let’s try those 10K random dice rolls from earlier, but now with an eager approach:
-- This works fine!
numbers : List Int
numbers =
List.range 0 10000
|> List.foldl numbersHelp ( [], Random.initialSeed 1234 )
|> Tuple.first -- don't need the seed anymore
numbersHelp : a -> ( List Int, Seed ) -> ( List Int, Seed )
numbersHelp _ ( acc, seed ) =
let
( newAcc, newSeed ) =
Random.step dieRoll seed
in
( newAcc :: acc, newSeed )
Oh look! That works! Looks like our reasoning by analogy pointed us to a working solution!
If we can solve our simplified 10K random dice rolls problem, we should also be able to use a similar solution for the original problem.
sprawlOut : Int -> Location -> R.Seed -> (( Location, Set Location ), R.Seed)
sprawlOut depth loc seed0 =
List.foldl
(\_ (acc, nextSeed) -> R.step (sprawl acc) nextSeed)
(( loc, Set.empty ), seed0)
(List.range 1 depth)
sprawl : ( Location, Set Location ) -> Generator ( Location, Set Location )
sprawl ( loc, set ) =
R.uniform loc (neighborsOf loc)
|> R.map (\next -> ( next, Set.insert next set ))
It’s not particularly nice, but it works! Success!
See the final solution in action
Conclusion
Several debugging techniques were used in the course of solving this problem. Simplifying the problem is always a good place to start. It’s a variation on reasoning by analogy, although analogies are allowed to be more than just simplified versions of your original problem.
When you’re debugging a problem, you will have a lot of assumptions. Test all of them and attempt to disprove them.
Look at your code and try to list the ways it could break. Then go through them all and try to see if they can trigger your bug. Use process of elimination to narrow the focus of your search. Make sure to test all your assumptions along the way though!
Once you have some data about some combinations that work and some that break, ask yourself “how are these the same?” and “how are these different?”.
Discussion around stack overflow seen in this article and its solution led to a
PR against Random.Extra to add some stack-safe helper functions.
